By Tom McHale
Tom shows you some tools and tricks to calculate the distance to a target when long range shooting.

USA –-(Ammoland.com)- In the previous two parts of the Long Range Shooting Guide, Theory and MOA, Mils and Math, we talked about how to account for distance.
Gravity exists for most sober people, so we shooters have to “lob” our shots a little or a lot depending on how far away a target is. Last time we talked about figuring out exactly how much to lob with scope adjustments.
What we haven’t yet discussed is how to figure out the distance in the first place.
If you’re at a competitive shoot range, figuring out the distance variable is easy – just look at the match program or ask the guy or girl next to you. In the field, things become slightly more complicated if you’re not in a position where you can pace off the steps. If you like gadgets and have a little extra coin, you can always invest in one of the niftiest electronic tools ever, a laser range finder.
You can get a dedicated range finder that does nothing else, like many Bushnell Rangefinders. You can get a fancy one that interfaces with a Kestrel weather meter and ballistic computer.


That’s a point-and-shoot solution. Just laser the target and the rangefinder beams distance and shooting angle information to the weather meter and ballistic computer. That, in turn, churns, rattles, and smokes until it spits out an answer that tells you exactly how to adjust your scope for that specific shot. You might also choose a set of binoculars with a rangefinder built in. This Bushnell Fusion model does exactly what, so if you’re out hunting, it’s one less thing to carry. When you’re glassing the area, a simple button press will also tell you the exact distance to whatever it is you’re looking at.

Those solutions are well and good, and I highly recommend them, but you ought to know how to find the distance the old-fashioned way too.
Over the holiday weekend, I had a reminder of how quickly the “manual” ways of doing things fade from our collective consciousness. While cruising around with my adult kids and nephews in a golf cart, we happened to get on a discussion of manual turn signals. After some very puzzled expressions, I figured that not one of them had ever heard of how to signal with your left arm out the window. It’s a good thing we still have electricity. Anyway, for when the batteries die, or you drop your fancy electronics into a canyon, or even if you just like doing stuff old school to show off and act crotchety, here’s how to calculate the distance with nothing more than your scope.
The whole concept is based on your proportion and your thumb. OK, so I used a math term, but don’t worry, there’s no need to do something rash like fake your own death, at least not just yet. While under the covers, there are impressive math concepts involving things like sines, cosines, and counting using all 23 toes and fingers, the concept is the same as estimating using your thumb. Let’s consider an example.
Unless I’ve recently smacked it with a hammer, my thumb is about .94 inches wide. When I stick it up at arm’s length, it’s about 27.5 inches from my eyeball. With these two important measuring tools, I have the beginnings of a range finding system. I can estimate, limited to the precision of my thumb, the distance to just about anything as long as I know the size of an object near my target. For example, there’s a picture on a wall in the room next to my office that’s 14 inches wide. I’ll just bet you’re wondering how far that picture is from my desk. Well, by holding up my thumb, I can figure it out. As it so happens, when I hold my thumb over that artwork, my thumb just barely covers it, so my .94-inch-wide thumb perfectly covers 14 inches at that distance, whatever it is. Using some proportional math like this, I can figure out the missing distance value.
If I use the 8th-grade algebra skills that Miss Lillynoggin taught me, I can rewrite that as:
If I solve for the unknown distance in that proportional relationship, I figure that the picture is 34.13 feet away. Using the very scientific “a pace is about three feet” method, I find that it is! You’ll have to trust me on that, or else you’ll have to call for an appointment to pace it off yourself.
Those measurements in scope reticles like milliradians and minutes of angle are way more precise and practical than the thumb method, but it works exactly the same way. As we talked about last time, a milliradian represents .36 inches at a distance of 100 yards while a minute of angle represents 1.04 inches at 100 yards. Think of those as either a .36-inch wide thumb at the end of a 100-yard long arm or a 1.04-inch wide one depending on whether you want to measure your thumb using mils or minutes of angle.
For easy math, let’s round a bit and call a minute of angle one-inch at 100 yards.
Now let’s get practical with that knowledge. I have sitting here a Burris XTR II Riflescope that has a reticle filled with about a billion hash marks going up and down the center crosshair. Each little mark is exactly one minute of angle apart from the adjacent ones. I get that information from the instructions that came with the scope.
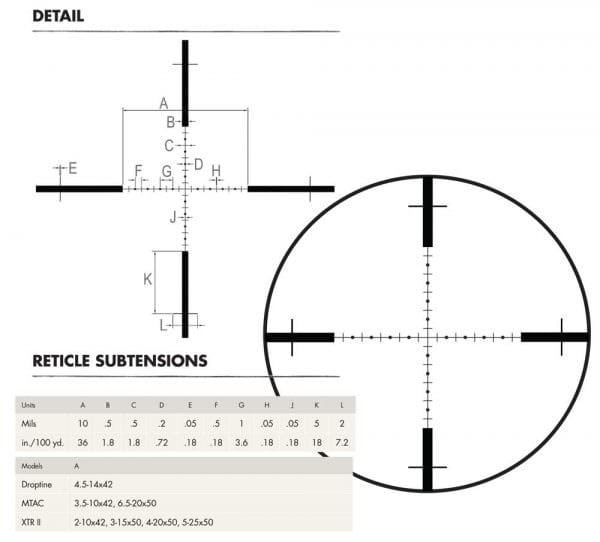
This is one time where even us guys should read the instructions first. If I look at a one-inch tall Oompa Loompa, and he appears to fit exactly in between two of those marks, then he looks to be one minute of angle tall when viewed through this scope. Since I know the marks represent one minute of angle, and I know that this particular Oompa Loompa is one-inch tall, I can calculate how far away he is. In this case, I know that he must be 100 yards away because one MOA is one inch at 100 yards. Here’s the math:
If our Oompa Loompa appears to be two MOA tall in the scope, using the same formula tells us that he is 50 yards away.
Using a scope that has MOA or mil (we’ll get to that in a minute) markings, you can find distances this way as long as you know the sizes of objects that are common your area that might be near your target. Here are some examples of things you can use:
- Fenceposts
- Deer (maybe average height from ground to shoulder or back)
- Vehicles or tires
- Signs
- Let’s continue with an example that uses this type of approach. Suppose fence posts of a certain type in your area are four feet (48 inches) tall. Using a scope with MOA markings, you can see a post that appears to be six minutes of angle tall through your scope. How far away is it? Let’s plug those numbers into the same formula we used before.
If you want to be precise and account for the fact that a minute of angle is actually 1.04 inches instead of one, then you can simply substitute 95.5 for the 100-yard figure like this:
This exact same concept works with scopes that use milliradian marks too; the numbers are just different. A milliradian translates to one yard at 1,000 yards, 36 inches at 1,000 yards, or .36 inches at 100 yards. Given the one-yard to one thousand ratio, it’s easier to use yards for your known object sizes. The standard formula looks like this:
So, using the same type of fence post for a different example, a four-foot fence post is 1.33 yards tall. If we see one that covers two mil marks through our scope, the distance calculation would be:
Once you know the marks available in your scope, you can get surprisingly precise with this stuff. Your optic manufacturer will have a diagram buried somewhere in the instructions that show lots of different measurements available in your scope reticle. For example, the mil dots themselves are usually .2 mils wide. Hashmark thickness is often .05 mils. Using information like this, you can make an accurate observation of exactly how an object measures in mils. For example, rather than rounding our fence post to “two mils” we might be able to determine that it looks to be 2.4 mils tall when viewed through the scope.
The more granular you can be with your observation, the more accurate your distance calculation will be.
One more thing. If you use a variable power scope, you’ll almost certainly need to do your distance estimating at maximum magnification unless your scope instructions say otherwise. While it’s a whole new topic for another day, most scopes use a second focal plane reticle, so magnification changes the math. If you have a fixed power or first focal plane scope, then you don’t have to worry about this.
Now pull the trigger.
About
Tom McHale is the author of the Insanely Practical Guides book series that guides new and experienced shooters alike in a fun, approachable, and practical way. His books are available in print and eBook format on Amazon. You can also find him on Google+, Facebook, Twitter, and Pinterest.






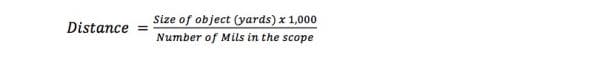
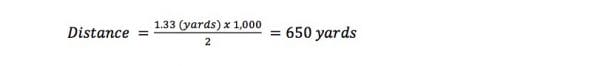

Interesting article, as a retired engineer found it very informative. As I said retired, I learned on a slide rule many decades ago ……. HA. So as interesting the mathematics are and the condition of these 6 decade old eyeballs, think I’ll stick with my Bushnell Scout DX 1000 ARC Laser Rangefinder. I do carry a spare battery just in case.
On something like a deer, you’ll be lucky to see it range at 800yds.
The figures quoted by rangefinder manufacturers are invariably for reflective or at least flat, white targets.
Only time I’ve managed 1,000yds (1,008 according to the range given) with my Leupold was off a white painted, stone farmhouse.
Best I’ve managed off deer/the back ground to deer, is a shade over 600yds.
From experience, take the manufacturer’s headline number, then subtract a third for real world shooting.
When my grandfather taught me to shoot many years ago he told me to try and see in my minds eye how many football fields were between us and the target. I think that your way is much more precise.